因式分解的单元教学思考

周志英：北京市十一学校 中学高级

因式分解是初中代数中的一个非常重要的内容。作为一种重要恒等变形的手段，它与乘法公式、分式运算、解一元二次方程、二次函数的顶点坐标以及降次、配方等知识方法有着十分密切的联系。

根据因式分解与各部分内容的不同联系，可以将这些联系分为因式分解在不同阶段的理解与因式分解在不同知识中的应用。这样，对于因式分解的理解可以分为以下三个螺旋上升的阶段：因式分解的概念、乘法公式与因式分解的关系、二次方程与因式分解的关系。而分式运算和二次函数这两部分内容是因式分解的应用。

在第一阶段，重点是帮助学生理解因式分解的概念，即理解因式分解与整式乘法的互逆性，根据因式分解的概念对多项式进行因式分解。

我们把一个多项式化成几个整式和积的形式，像这样的式子变形叫做把这个多项式因式分解。因此，因式分解与整式乘法是相反方向的变形。根据因式分解的概念，乘进去和提出来是互逆的，所以这一阶段，最基本的因式分解的方法是提公因法，或者说所有的因式分解的方法的本质都是提公因式法。

因式分解是整式乘法的逆向变形，单项式乘多项式的算理是利用乘法分配律，所以分解因式的算理是逆用乘法分配律，而提公因式法也就是把这个单项因式提出的过程。

如：整式乘法 与因式分解 。

而对于多项式乘多项式，运算过程是先把一个多项式看作整体，利用乘法分配律转化为单项式乘多项式。

如：

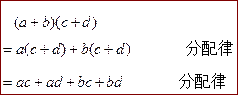
在上述运算过程中，虽然两次用的都是乘法分配律，但还是有所区别，第一次是把 看作一个整体用乘法分配律，第二次是局部应用乘法分配律。

将上述运算过程逆过来，整式乘法就变为了多项式的分解因式 。

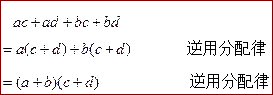
可以看到，在这个分解过程中，先局部提单项公因式，再整体提多项公因式 ，也就是说在这个分解过程中，先局部逆用整式乘法中的单项式乘多项式，再整体逆用整式乘法。

对于多项式乘多项式，最后的结果应是最简形式，所以乘法分配律后如果有同类项要合并。

如：

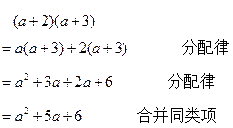
同样，将上述运算逆过来，就是因式分解的过程。

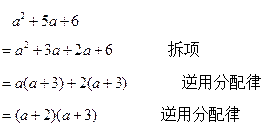
所以说，因式分解的本质是整式乘法的逆向变形，包括逆用乘法分配律和逆用合并同类项，其中乘法分配律是关键，因式分解过程中是否需要拆项，取决于能不能直接用逆用乘法分配律提公因式。所以从这个角度来说，提公因式法是分解因式的通法。

我们再试着用上述方法将下列两个多项式分解因式。

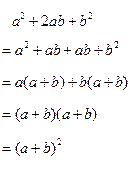
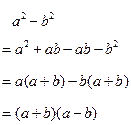
从整式运算来说，乘法公式 、 是多项式乘多项式的特殊情况，我们把它概括归纳为运算公式。所以因式分解中的公式法是也是因式分解的特殊情况，这也体现了我们在研究某一类数学问题时，常常选择一些特殊情况为代表来研究，如以二元一次方程组为代表学习消元，以一次函数、二次函数、反比例函数为代表来研究变量。

基于此，教材中大多向学生介绍了提公因式法这一通法和公式法这一特殊方法，前者的学习可以帮助学生理解因式分解与整式乘法的互逆关系，后者的学习可以帮助学生形成对代数式进行结构分析的意识与能力。

在第二阶段，对于因式分解概念的进一步理解。因为因式分解与整式乘法是互逆的，所以整式乘法有两个重要的公式——平方差公式、完全平方公式，那么对于由这两个公式运算出来的多项式也可以直接逆用公式化成乘积形式。因此，我们得到了因式分解的两个重要方法——公式法。

平方差公式：

完全平方公式：

在这一阶段，我们要帮助学生理解并掌握两个公式的结构特征，在利用公式法因式分解时，根据所分解的多项式的项数以及每一项的特点，选择相应的公式。

特别要注意的是，利用完全平公式不仅可以将一类三项式分解因式，更重要的是还可以利用它通过配方将一个二次三项式部分因式分解，进而可以对这个二次式的非负性进行研究。

如探究多项式 的最值。

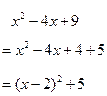
所以当 时，多项式 有最小值是 5。

另外，有了配方法，对于一个不能直接用完全平方式进行因式分解的多项式，我们可以通过先配方再利用平方差公式进行因式分解。

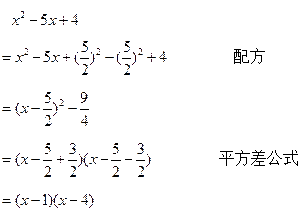
在第三个阶段，是因式分解与一元二次方程。在前两个阶段，我们只能将可分解的多项式因式分解，但不能解决“在实数范围内，什么样的二次式可以因式分解，什么样的二次式不能分解”这个问题。在一元二次方程中，我们不仅可以借助于因式分解将二次方程转化为两个一次方程，而且可以利用方程的根进行因式分解，最重要的是还可以利用判别式判断一个二次式能否在实数范围内分解因式。

对于 ，当 时，方程有两根 和 ，此时多项式 在实数范围内可以因式分解，即 。其中，当 时，两根 和 相等， 或 。

所以，对于因式分解的学习，是贯穿于初中整个代数的学习，对于学生而言，是个循序渐进的过程。