“反比例函数的图象与性质”说课

见海荣：首都师范大学附属育新学校 中学高级

一、教材分析：

1. 反比例函数是刻画和研究现实世界变化规律的一类重要的数学模型，在物理、化学等自然科学中有着广泛的应用。

2. 对于反比例函数图象及性质的研究与学习，尽管还处于函数学习的初级阶段，但它所体现的函数学习的一般规律和方法，是继一次函数、二次函数学习之后的再一次强化。

3. 反比例函数图象和性质的学习，由于自变量参与的运算与前面函数的截然不同，所以也是知识与方法上的一次拓展，理解与认识上的一次升华，思维上的一次飞跃。

4. 反比例函数的图象和性质，蕴含着丰富的数学思想，是“数”与“形”的统一体，又充分体现了变化与对应的数学思想。

5. 通过反比例函数图象及性质的研究与学习， 可以使学生对分式、分式方程等数学模型的认识进一步完善，更是对分式运算的能力的提升。

二、学情分析

1. 本节课是在已经学习了平面直角坐标系和一次函数的基础上，进一步研究反比例函数的图象和性质，学生具备研究函数的图象和性质的一般方法知道研究函数的图象和性质的一般程序，这对于学习反比例函数的图象和性质做出了良好的铺垫。

2. 同时反比例函数图象和性质的学习中，图象由“一条”到“两支”，形态由“直”到“曲”，由“连续”到“间断”，由与坐标轴“相交”到“渐近”，这些对学生而言是继一次函数后，知识与方法上的一次拓展，理解与认识上的一次升华，也是思维上的一次飞跃 ,因此是学生学习的难点。

3. 借助解析式定量分析反比例函数的性质建立在学生对式的运算准确的把握的基础上，而对式的运算准确的把握学生有些薄弱，所以这也是学生学习的难点。

三、目标分析

基于以上两个内容，我确立了如下教学目标：

[ 知识技能 ]

会画出反比例函数 的图象了解其特征 .根据反比例函数的图象和解析式探索并理解探索 和 时，图象的变化情况及其性质。

[ 数学思考 ]

在探索反比例函数的性质过程 发展学生观察、分析、比较、抽象及概括能力，进一步培养学生运算能力，发展几何直观 。

在正比例函数 与反比例 的类比过程中体验类比思想， 在探索性质中感悟、“变化与对应”、“数形结合”的数学思想，在问题解决中体会“分类讨论”的数学思想方法。

[ 问题解决 ]

通过对 反比例函数的定性和定量研究，使学生初步感受和理解研究函数的一般方法。

[ 情感态度 ]

在探究活动中形成严谨的科学态度和勇于探索的科学精神，学会与人合作交流，学会倾听、欣赏和感悟。

[ 重点 ]

会 画出反比例函数的图象 ,理解反比例函数的性质。

[ 难点 ]

准确画出反比例函数的图象，借助解析式定量分析反比例函数的性质。

四、过程设计

（一） 回顾方法 确定过程

教师通过问题引导学生类比已学过的一次函数的图象和性质的研究过程，明确研究反比例函数的图象及其性质的一般方法，从而明确研究过程。

1. 对要研究地函数根据系数的取值范围进行分类；

2. 一般问题特殊化 , 通过具体函数 定性（图象）、定量（解析式）两个角度研究性质。

3. 通过改变 中 的值，如分别取 为 ， 然后特殊问题一般化归纳性质。

（二） 定量定性 探究性质从抽象到具体才有助于进行探索 ,为了 获得反比例函数 的性质，教师采用“一般问题特殊化”的基本策略 ,引导学生具体研究反比例函数 图象和性质。

1. 结合反比例函数 的列表过程，引导学生找出自变量 的取值范围，并发现自变量 每取一个值，函数 都有唯一确定的值和它对应，对于 在某一范围内的取值，即当 或 时，函数值的取值范围以及 随 的变化规律，从而得到关于函数性质的猜想。

2. 请学生描出表格中的点的位置 , 并利用计算机展示 的图象，帮学生突破画 的图象这一难点，从而正确画出反比例函数 的图象，然后引导学生借助直观的图象描述函数的性质。

3. 教师引导学生由解析式证明上述性质的正确性。这一环节有两个难点：难点之一是关于的范围的分情况讨论；若点 在反比例函数 图象上，则 的大小有以下三种情况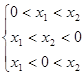： 其中情况学生最容易忽略， 这需要教师进行耐心的引导和点播；难点之二是借助解析式定量分析反比例函数的性质建立在学生对式的运算准确的把握的基础上，而对式的运算准确的把握学生有些薄弱， 所以这也是学生学习的难点。如，要比较这两个数的大小，教师可以引导学生用作差法化解难点。

这样的设计，让学生由列表法猜想性质、借助图象描述性质、由解析式证明性质，是学生充分体验变化与对应、数形结合的思想方法， 培养了学生的观察、分析、抽象、概括的能力，发展了几何直观能力，同时这一过程更是对分式运算的巩固与提升。

（三）深入探究 一般结论

为了使学生进一步体会“一般问题特殊化”这一问题解决策略，认识研究数学问题的一般方法 :虽然特殊无法代替一般，但是在众多特殊中却蕴含着一般的规律。教师通过问题引导学生思考 是否所有的反比例函数的图象都具有上述性质，引导学生分组尝试改变 中 的值，如分别取 为 时画出反比例函数图象。 观察所得到的不同的反比例函数图象的特征及函数性质，引导学生归纳“变化中的规律性”。然后，从解析式的角度，引导学生分析上述结论的合理性，从而得到反比例函数 图象的特征与函数性质。

这一环节，学生了经历从特殊到一般的认识过程，加强了对反比例函数图象“特征”和函数“特性”以及它们之间的相互转化关系的认识，更通过归纳，培养学生抽象概括能力。

（四）应用性质 解决问题

为了学以致用，教师设计了如下问题：

问题（ 1）若点 、点 在双曲线 上，则 与 的大小关系是 ；

（ 2）你能在原题的基础上进行修改，也设计一道题目吗？

对问题（ 1）学生可能会用到代入求值法、直接利用函数增减性或利用函数示意图等不同方法解决问题 , 代入求值法可使学生提高也能算能力 ,直接利用函数增减性无疑巩固了学生对性质的认识 ,利用函数示意图解决问题则使学生进一步体会数形结合的思想方法。教师引导学生交流解决方法，提升学生认识。对于问题（ 2），学生改编问题可能有如下方向：换 A、 B点的横坐标，同负，异号等；或换 的值，取个具体的负值 ;或将题目条件进一步一般化为： 若点 点 在双曲线 上，且 ,则 与 的大小关系是 。开放性的问题设计，可以使不同同学根据自身认知水平提出不同问题，有利于培养学生提出问题的意识，也渗透数学问题研究的一般方向。

( 五 ) 总结收获 提出疑惑

本环节教师引导学生反思学习过程，使学生对反比例函数的图象与性质这一知识有较为整体全面的认识，同时体会本节课用到的研究问题的一般方法及领悟到的数学思想方法，同时鼓励学生大胆提出自己的疑问，可能还有学生提出 对图象的影响或是提出类比一次函数 中 的几何意义，反比例函数中 的几何意义是什么等问题 ,这些可以留作课后的思考题目 ,既可以深化学生对知识的认识 ,更能使保持良好的探究欲望，这样的环节更有利于学生养成良好的数学学习习惯。

五、教学反思

希望通过本课时的教学，使学生在以下三方面认识有一定发展： 1. 深化函数概念的认识，体会变化与对应； 2.类比正比例函数的研究，进一步感受研究函数的一般方法； 3.在教学的每个环节时刻注意引导学生体解析式，图象，性质三位一体的地位，引导学生根据不同问题，从不同的角度解读，感受自变量与函数值之间变化与对应的关系； 4.关注反比例函数对分式运算能力的提升作用。